Movimiento parabólico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical
Tipos de movimiento parabólico
[editar] Movimiento parabólico (completo)
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
[editar] Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.
La velocidad inicial se compone de dos partes:
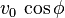 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
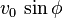 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
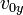
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
[editar] Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:
que es vertical y hacia abajo.
[editar] Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Derivación de la ecuación de la velocidad
|
|---|
|
Partimos del valor de la aceleración de la gravedad y de la definición de aceleración y tenemos Separamos variables y pasamos a la integración efectuamos las integrales Sustituimos |
Esta ecuación determina la velocidad del móvil en función del tiempo, la componente horizontal no varía, mientras que la componente vertical sí depende del tiempo y de la aceleración de la gravedad.
[editar] Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando de la siguiente ecuación diferencial:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
| [mostrar]
Derivación de las ecuación de la posición
|
|---|
|
Partiendo del valor de la velocidad y de la definición de velocidad, calculamos el vector de posición así tenemos: esto es: integrando: descomponiendo la integral: sacando términos constantes de la integral: realizando la integral: ordenando términos: donde que sustituyéndolo en la ecuación resulta: y ordenando, por fin: |
La trayectoria del movimiento parabólico está formada por la combinación de dos movimientos, uno horizontal de velocidad constante, y otro vertical uniformemente acelerado; la conjugación de los dos da como resultado una parábola.
Movimiento parabólico con rozamiento
Cuando consideramos el rozamiento la trayectoria es casi una parábola pero no exactamente. El estudio de la trayectoria en ese caso es considerado por la balística




 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.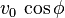 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.

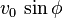 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
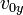
 : [ecu. 1]
: [ecu. 1]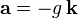
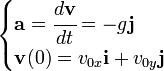





 [ecu. 1], por su valor
[ecu. 1], por su valor
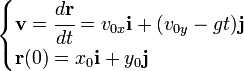










 es el vector de posición del móvil para el instante t = 0, podemos dividirlo según sus componentes en:
es el vector de posición del móvil para el instante t = 0, podemos dividirlo según sus componentes en:

